2.2 The Factor Theorem, Synthetic Division, and the Difference and Sum of Cubes

Synthetic Division

Synthetic Division is a shortcut for long division of polynomials. It saves time, energy, effort, and paper, and because math homework consumes a lot of all of these limited resources, it is in our best interest to use this efficient method of dividing polynomials.

We begin with an equation, the dividend. Ensure the dividend is in order of descending exponents.



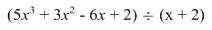
Take the divisor, set it equal to zero, and isolate x.
0 = x + 2
-2 = x

Synthetic division will take four lines. On the left side of the second line, write -2 inside a _|. This will be the multiplier. On the first line, indented so that it is not over the -2, write the dividend with plenty of space between the terms.

In the end, we will have this:



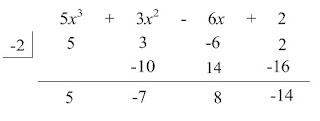
How? Using a different diagram for easier understanding, we can see the process:



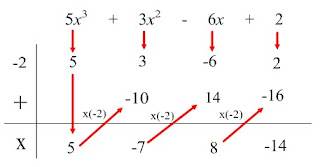
(A) Bring down the coefficients of each term, and the constant, in the same order as they are already in.

(B) The leftmost number is brought down and written. [It is the same as 5 + 0, as 0 is the previous term's coefficient (0x^4)].

(C) The sum is multiplied by -2 (or whatever number is in the corner) and written below the next number.

(D) The number you just wrote is added to the number above it, and written under the line.


The numbers, in order, are 5, -7, 8, and -14. The rightmost number is the remainder. The one to the left of it is the constant, the one to the left of that is the coefficient of the x-value, and the one to the left of that is the coefficient of the x^2 value. The quotient is 5x^2 - 7x + 6 with a remainder of -14.

Therefore the equation is
5x^3 + 3x^2 - 6x + 2 = (x - 2)(5x^2 - 7x + 6) - 14


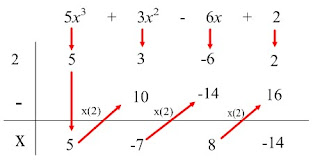
This is the Burchat Method of Synthetic Division. Alternatively, we can use the Textbook Method of Synthetic Division (found on pg 98 of your textbook).

When using the TMoSD, we don't have to find the x-value that ensures x + n = 0 is true. Instead, n is taken in its current form and used. Then, in step (D), the numbers in the third line are subtracted from the numbers in the second line.



The Factor Theorem

The factor theorem is a shortcut to finding the factors of a polynomial.

It goes like this:
"If x = a is substituted into a polynomial for x and the remainder is 0, then (x - a) is a factor of the polynomial."

We can use the remainder theorem to determine whether the remainders of the factors are zero.

The equation is f(x) = x^3 + 2x^2 - x - 2.


f(3) = 3^3 + 2(3)^2 - 3 - 2
f(3) = 27 + 18 - 3 - 2
f(3) = 40
.: (x-3) is not a factor

f(2) = 2^3 + 2(2)^2 - 2 - 2
f(2) = 8 + 8 - 2 - 2
f(2) = 12
.: (x-2) is not a factor

f(1) = 1^3 + 2(1)^2 - 1 - 2
f(1) = 1 + 2 - 1 - 2
f(1) = 0
.: (x-1) is a factor

f(0) = 0^3 + 2(0)^2 - 0 - 2
f(0) = 0 + 0 - 0 - 2
f(0) = -2
.: x is not a factor

f(-1) = (-1)^3 + 2(-1)^2 - (-1) - 2
f(-1) = -1 + 2 + 1 - 2
f(-1) = 0
.: (x+1) is a factor

f(-2) = (-2)^3 + 2(-2)^2 - (-2) - 2
f(-2) = -8 + 8 + 2 - 2
.: (x+2) is a factor

f(-3) = (-3)^3 + 2(-3)^2 - (-3) - 2
f(-3) = -27 + 18 + 3 - 2
f(-3) = -8
.: (x+3) is not a factor.

The factors are (x + 1), (x - 1), and (x + 2).

We can check by multiplication:

(x + 1)(x - 1)(x + 2)
= (x^2 - x + x - 1)(x + 2)
= (x^2 - 1)(x + 2)
= x^3 + 2x^2 - x - 2


While it may seem that it could take forever to find the factors, because you could plug in any number as the a-value, you can cut down the number of possibilities. The -a-value is always a factor of the constant in the polynomial. The -a-values all, when multiplied by each other, equal the constant.


Why does this work? Remember that the zeroes are also the roots, or the x-intercepts, of the polynomial graph. Where y=0, the x-value (x=a) is the x-intercept.



Difference and Sum of Cubes

Like a difference of squares, there is an easy way to find the factors of a difference of cubes. In addition, we can do the same with a sum of cubes.

First, the polynomial must be identified as a sum or difference of cubes. The first step is to look between the two terms and determine which sign separates them. The following rules are only applicable if the sign is + or -, and there are separate but similar rules for addition and subtraction. Then the terms must be identified as cubes, which can be done by finding the cube root of each term and seeing if they are integers. This is also useful because the cube roots will be used in the process of finding the factors.

The following equation is used to find the difference of cubes:



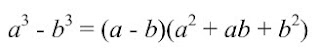
The following equation is used to find the sum of cubes:



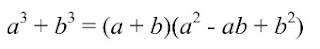
As you can see, the equations are very similar. It is important not to mix them up.


For the example, we will use the equation 64x^3 - 125.

Following the equation above,
a^3 = 64x^3
b^3 = 125

By finding the cube root of 64x^3 and 125, we can find the a and b values. In this case,
a = 4x
b = 5.

First, to find the difference of these cubes,

Sub a^3 = 64x^3, b^3 = 125, a = 4x, and b = 5 into a^3 - b^3 = (a - b)(a^2 + ab + b^2)

64x^3 - 125 = (4x - 5)[(4x)^2 + (4x)(5) + 5^2]
64x^3 - 125 = (4x - 5)(16x^2 + 20x + 25)

Next, to find the sum of these cubes,

Sub a^3 = 64x^3, b^3 = 125, a = 4x, and b = 5 into a^3 + b^3 = (a + b)(a^2 - ab + b^2)

64x^3 + 125 = (4x + b)[(4x)^2 - (4x)(5) + 5^2]
64x^3 - 125 = (4x + 5)(16x^2 - 20x + 25)