3.4 Solving Rational Equations, Solving Rational Inequalities – Period 1

Today’s lesson was about solving rational inequalities and equations

How to solve rational Equations:

Technically what are you doing? You are trying to find the value of x that allows both equations to be equal.
Example:
Graphically:
1) Graph both equations.
2) Find the point(s) of intersection (POI)
3) State the restrictions
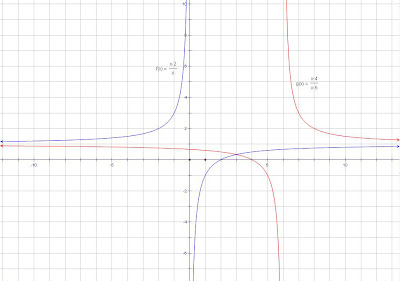The red line represents f(x) = (x-4) / (x-6)
The blue line represents g(x) = (x-2) / x
As you can visually inspect, the point of intersection is at x = 3.

⁂ x = 3, when x ≠ 0, 6

Algebraically:
1) Factor numerator and denominator if necessary
2) Cross multiply
3) Simplify to obtain polynomial equations
4) Solve for x
5) State the restrictions

How to solve rational inequalities:

Technically what are you doing? You are trying to find the values of x that satisfy the equation.

Example:
1) Bring all values to one side, resulting on one side equaling to 0

2) Simplify and factor the numerator and denominator
3) Find the vertical asymptotes, zeros, and restrictions

Vertical asymptotes: x = -5, -6
Zeros: 4, -1

4) Create a number line
5) Plot the vertical asymptote, zeroes (These are the factors the can affect the sign of the function)
6) Use test points to determine the sign of the expression in each interval.
7) State the solution


*NOTE: an equality symbol acts like an equal sign. However, DO NOT crosses multiply, when solving rational inequalities. When multiplying an inequality by a negative value, the greater or less than sign must be switched around.

Algebraically Summary:

1) Bring all values to one side, resulting on one side equaling to 0
2) Simplify and factor the numerator and denominator
3) Find the vertical asymptotes, zeros, and restrictions
4) Create a number line
5) Plot the vertical asymptote, zeroes (The function may change at the zeros or at vertical asymptotes. )
6) Use test points to determine the sign of the expression in each interval.
7) State the solution, with the restriction.

This is the file for the above note